
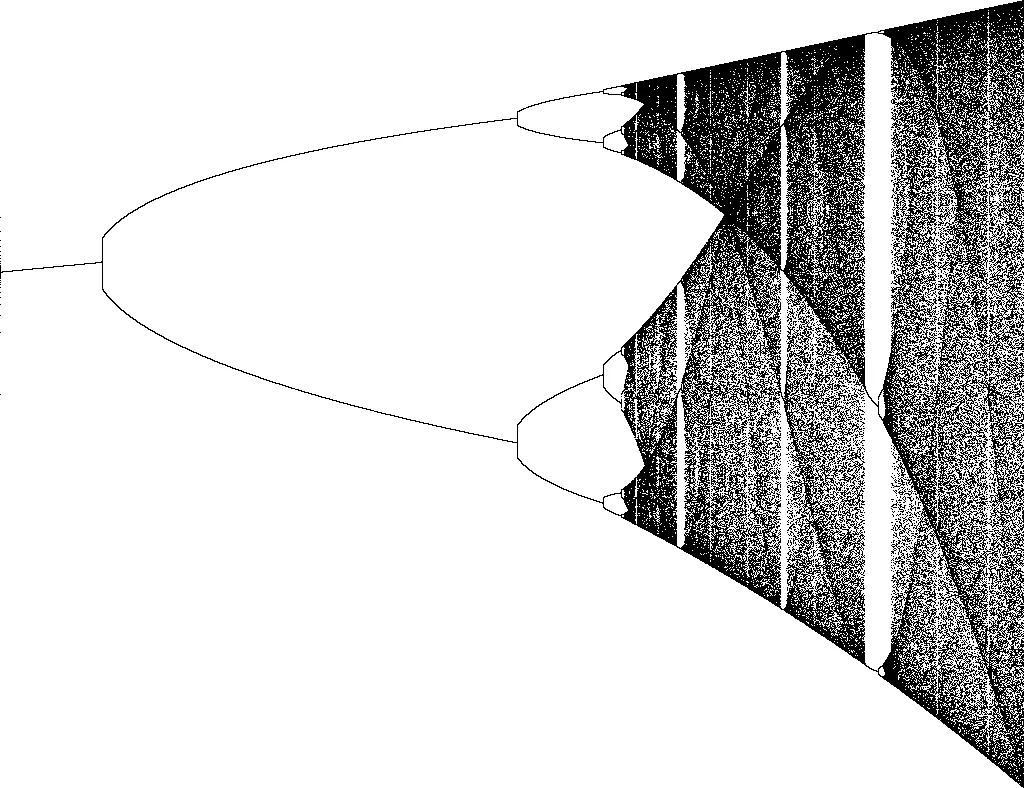
Bifurcation Diagram
2020
Letztens habe ich mich einem kleinen, lustigen Projekt gewidmet. Mein Ziel war es eine Bifurkation (oder auch Verzweigung) zu visualisieren. Die Bifurkation, die ich zeichnen möchte, ist eine der bekanntesten: Es ist die, für die logistische Gleichung . Aber bevor ich starte über das Programm zu reden, möchte ich erste ein paar mathematische Hintergründe erklären.
Als aller erstes, eine Bifurkation ist das verdoppeln einer Periode, welches auftritt, während man einen Kontroll-Parameter verändert. In diesem Falle ist der Steuerparameter , und die Verzweigungen tauchen, wie bei vielen anderen Beispielen, in einem festen Verhältnis auf: der Feigenbaum-Konstante. Während man r um einen kleinen Betrag bis 4 erhöht, kann man sehen, dass bei sich der Graph aufteilt. Bei , teilen sich beide Arme des Graphs erneut, diesmal in eine Periode von . Das geht so immer weiter, bis bei das deterministische Chaos beginnt.
Um diese Frage zu beantworten, müssen wir die Funktion, die die logistische Gleichung beschreibt, von einem anderen Winkel aus betrachten.
Hier ist noch einmal die Funktion: . stellt eine derzeitige Population. Aber nicht in einem absoluten Wert, sondern in einem relativen Wert zum theoretischen Maximum. Zum Beispiel ist eine diesjährige Population von Hasen. ist der theoretische Maximalwert. Dieser ist definiert durch die Natur, ein beeinflussender Faktor ist zu Beispiel der verfügbare Platz. Jetzt möchte ich die Population für das nächste Jahr berechnen.
Dafür muss ich den Wert von . wissen. In diesen Fall ist die Wachstumsrate. Wenn man nur den Parameter nehmen würde, dann wäre das Ganze ein lineares System. Für nimmt die Population mit der Zeit ab und stirbt irgendwann ganz aus. Für ,nimmt die Population unendlich zu. In der Natur ist das nicht der Fall. In jedem Jahr sterben Hasen, sei es durch Feinde oder auch nur Altersschwäche. Der Term repräsentiert genau diesen Rückgang der Population. Außerdem wird dadurch die Gleichung auch in ein dynamisches System umgewandelt. Man merkt eventuell auch, dass die Population im nächsten Jahr ausstirbt, wenn das theoretische Maximum von erreicht wird.
Nehmen wir eine Population von mit einer Wachstumsrate von . Setzt man nun diese Werte in die Gleichung ein, erhält man im nächsten Jahr eine relative Population von . Danach und wenn man immer weiter über diese Gleichung iteriert, wird man sehen, dass sich die die Größe der Population kaum/gar nicht mehr verändert. Das bedeutet die Gleichgewichtspopulation liegt bei . Das ist der Fall für , nicht jedes Mal , aber die Gleichgewichtspopulation wird sich bei einem Wert einpendeln.
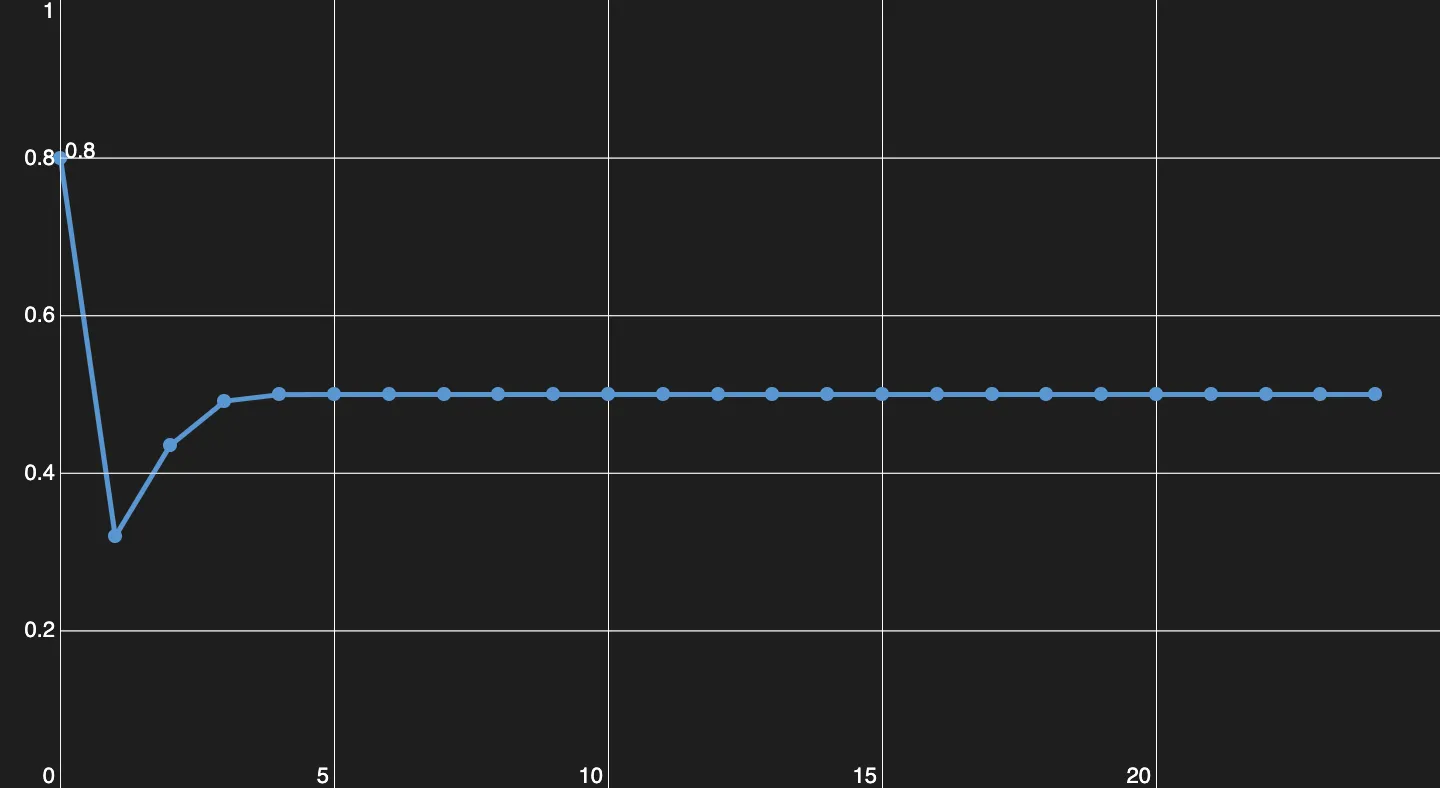
Hier sieht man, wie sich die Population entwickelt. (Für r = 2)
Setzt man nun in der Funktion ein, verdoppelt sich das erste Mal die Periode. Nun pendelt die Gleichgewichtspopulation zwischen Werten hin und her.
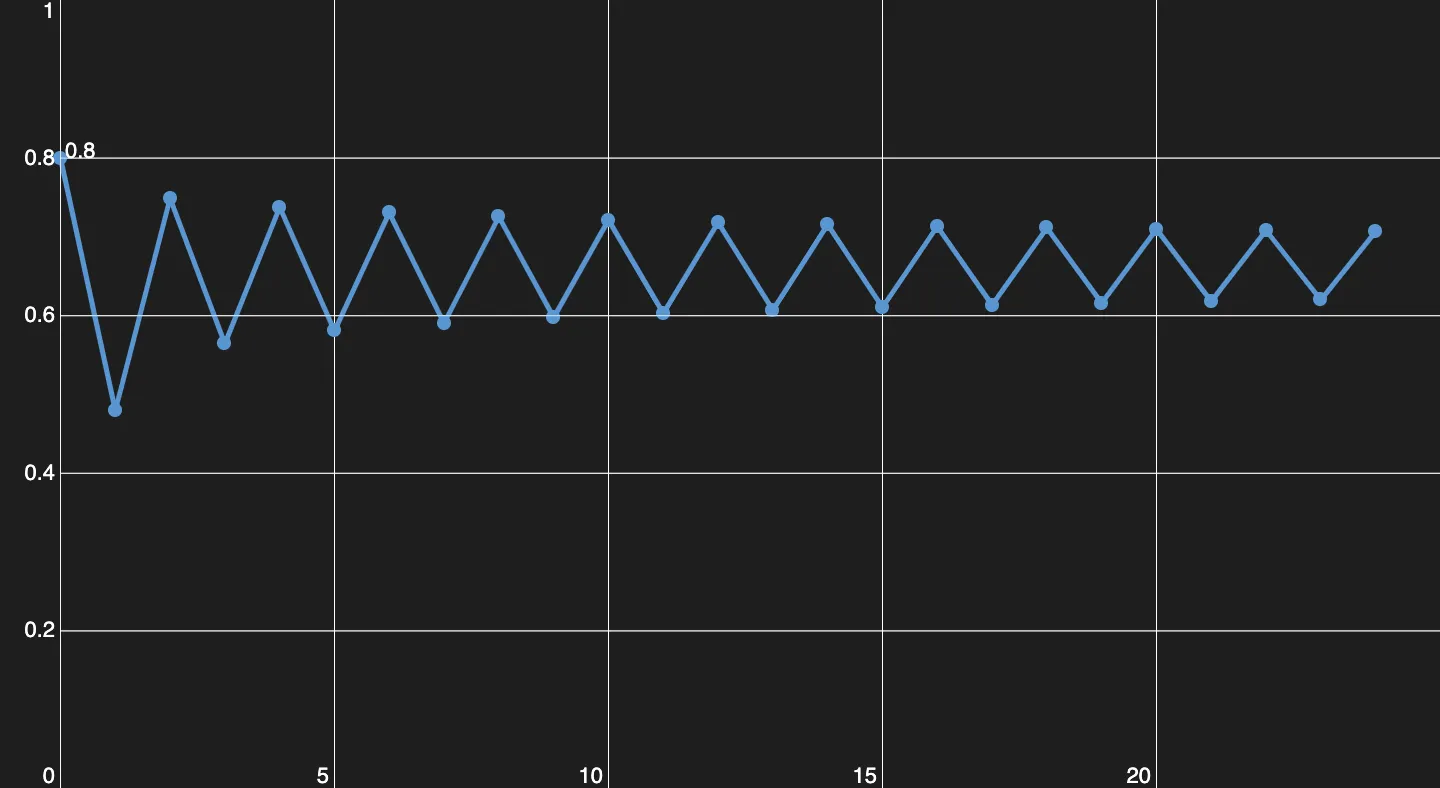
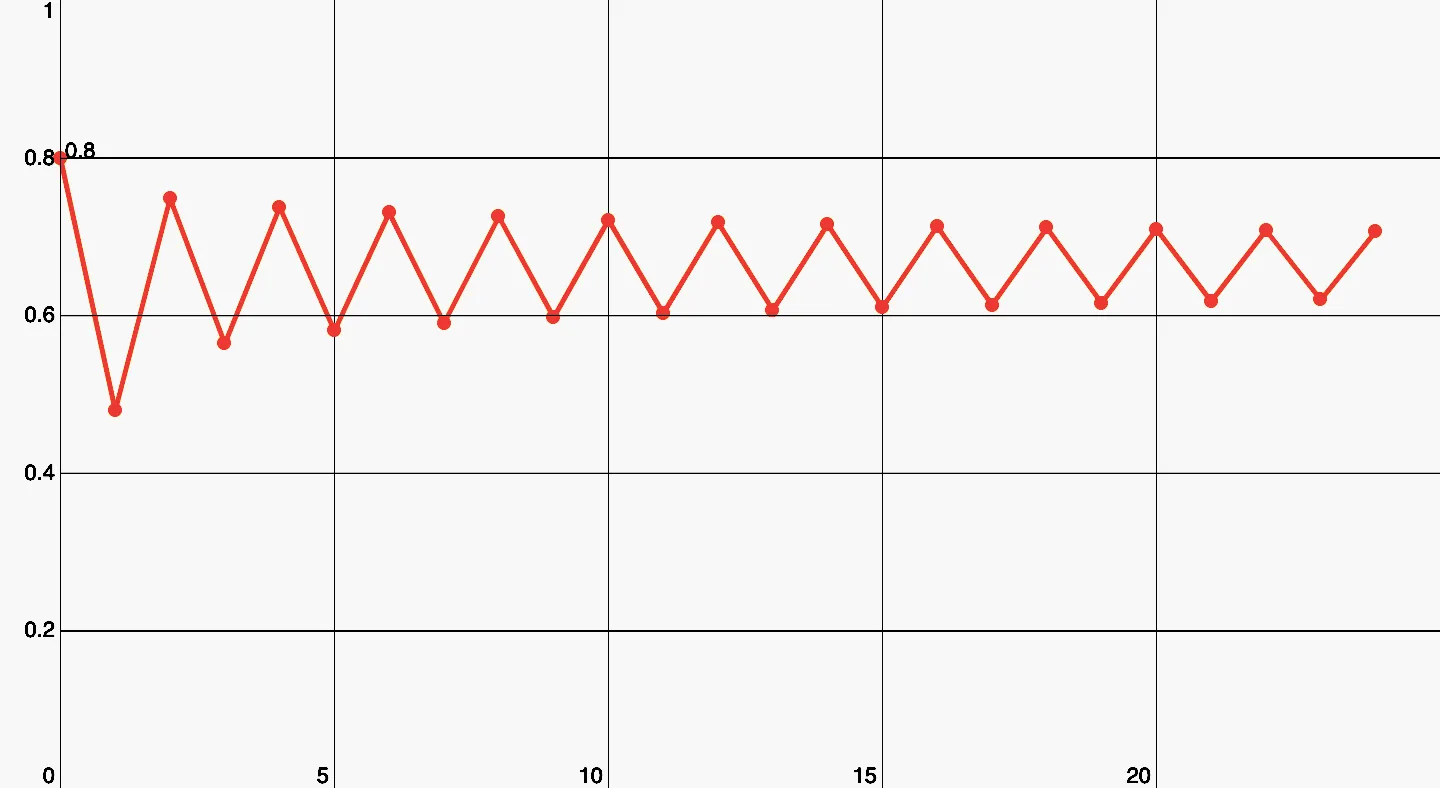
Hier sieht man eine Periode von 2.
Bei verdoppelt sich die Periode wieder, jetzt pendelt die Gleichgewichtspopulation zwischen Werten.
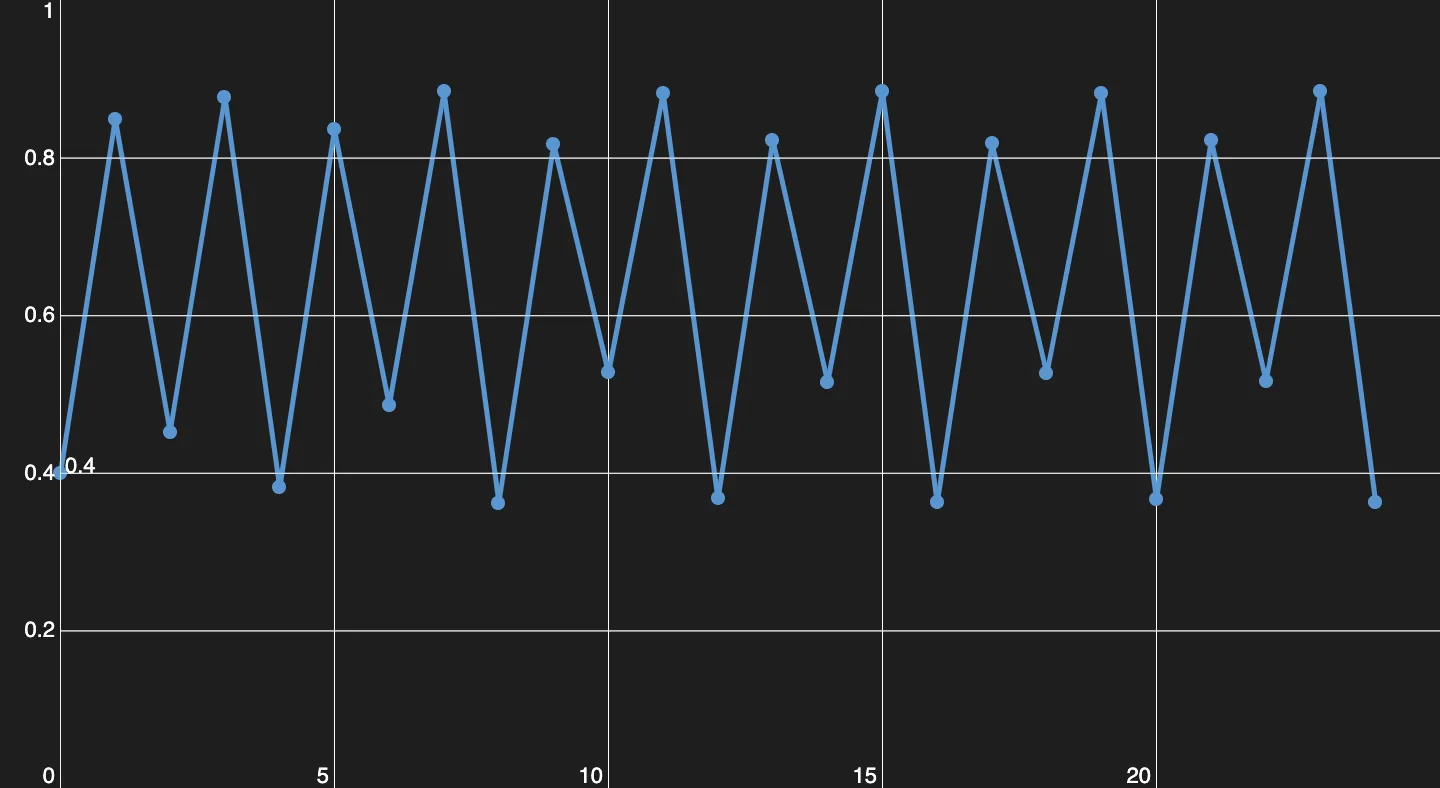
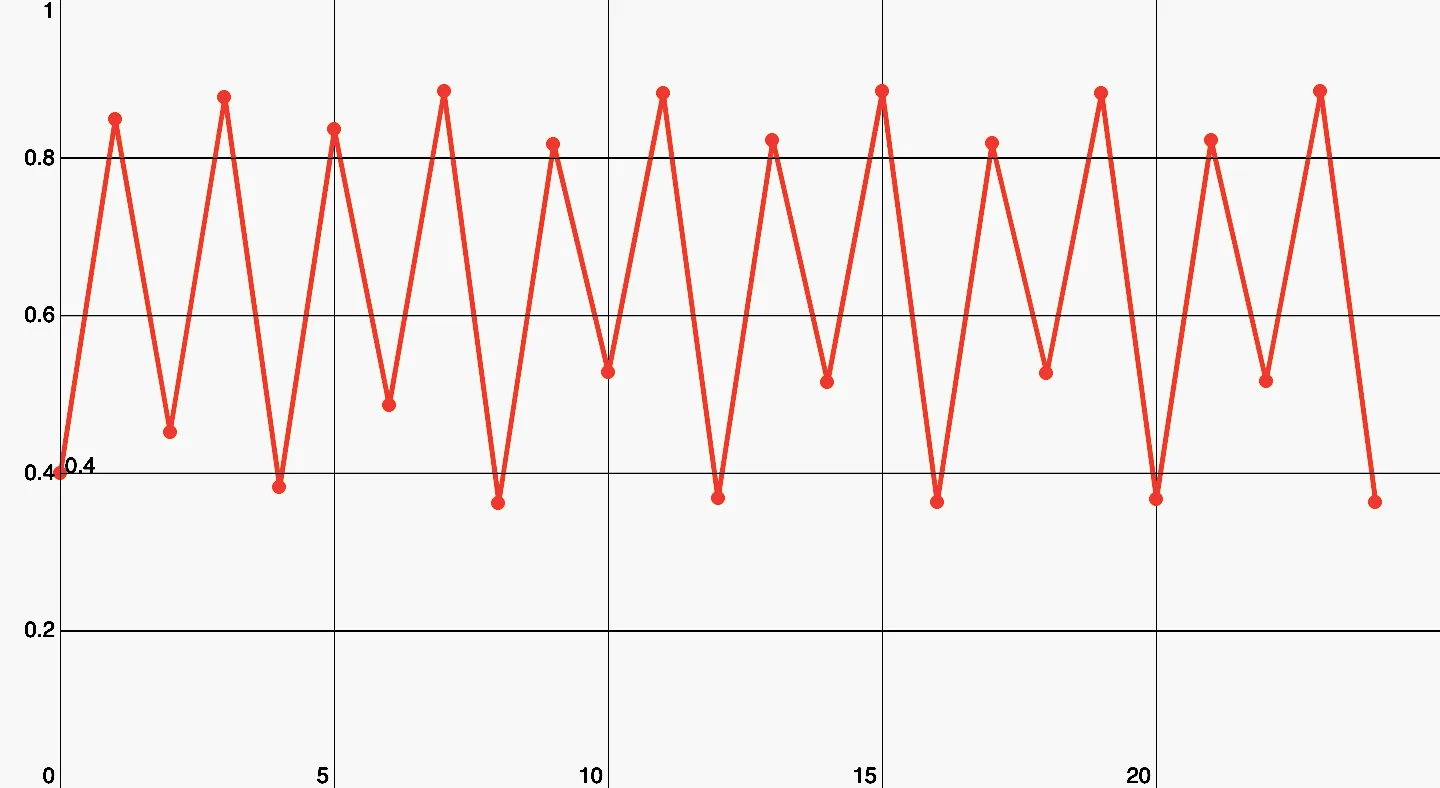
Danach kommt eine Periode von 4.
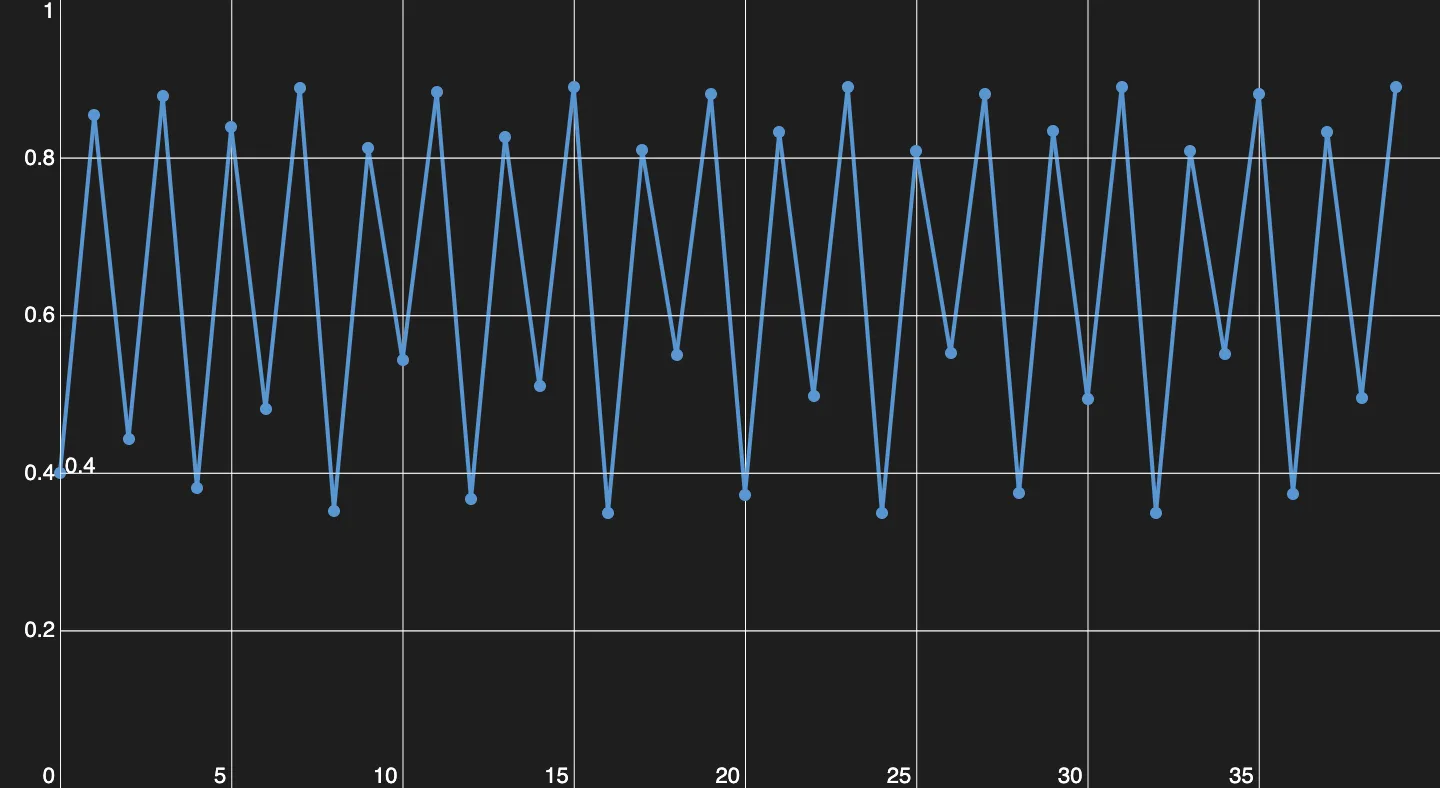
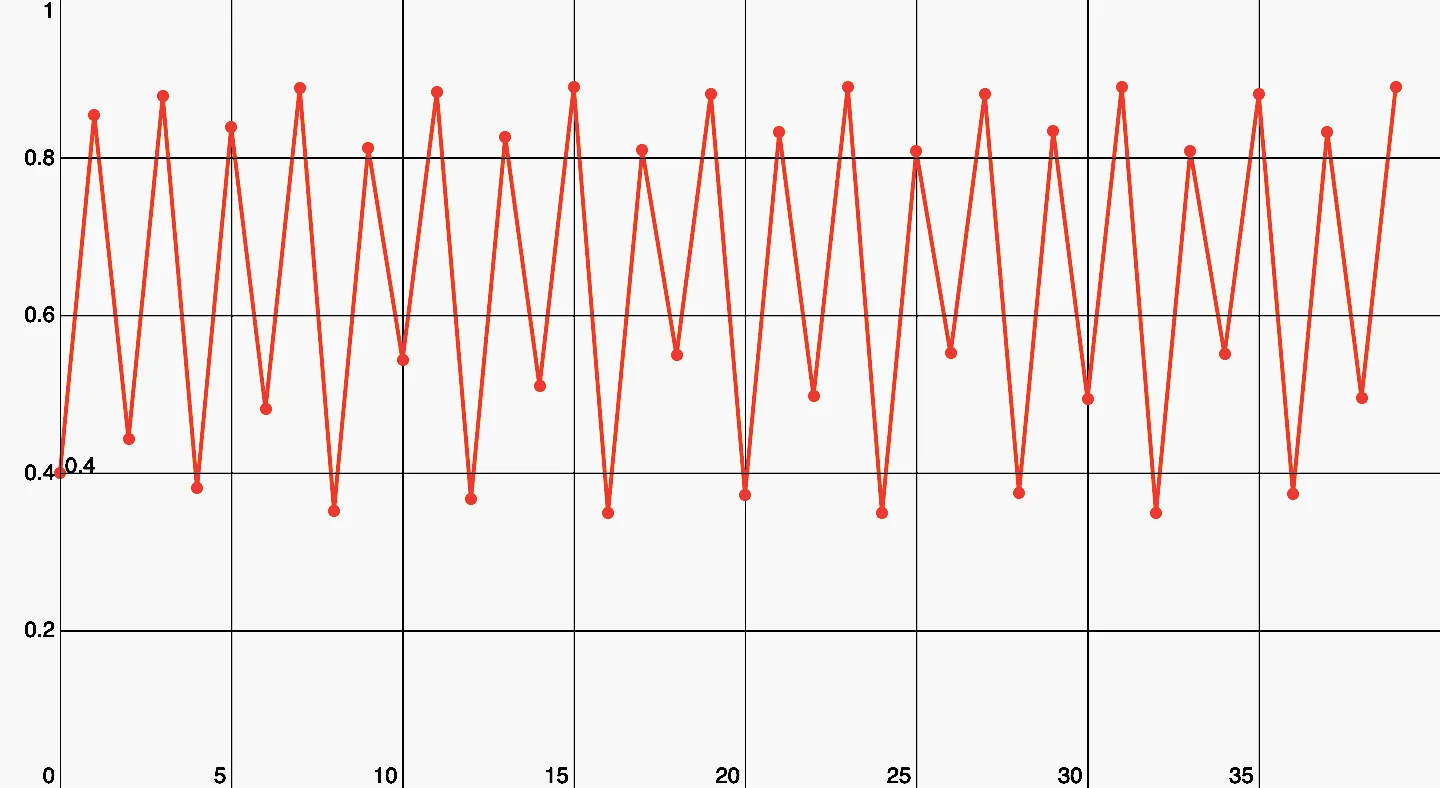
Eine Periode von 8. Es ist verrückt, wie eine so einfache Funktion, Muster wie diese erzeugen kann.
Letztendlich bei startet das Chaos.
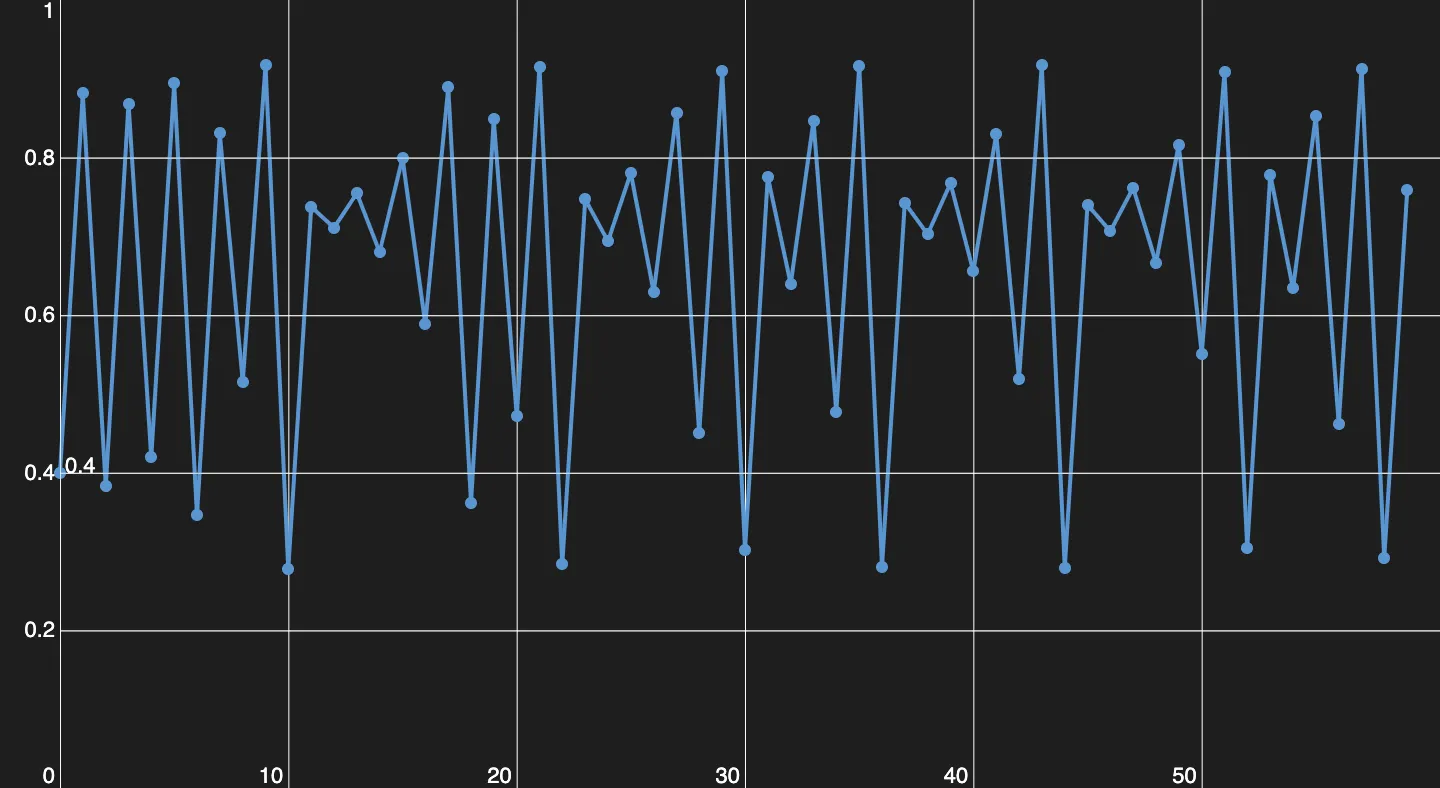
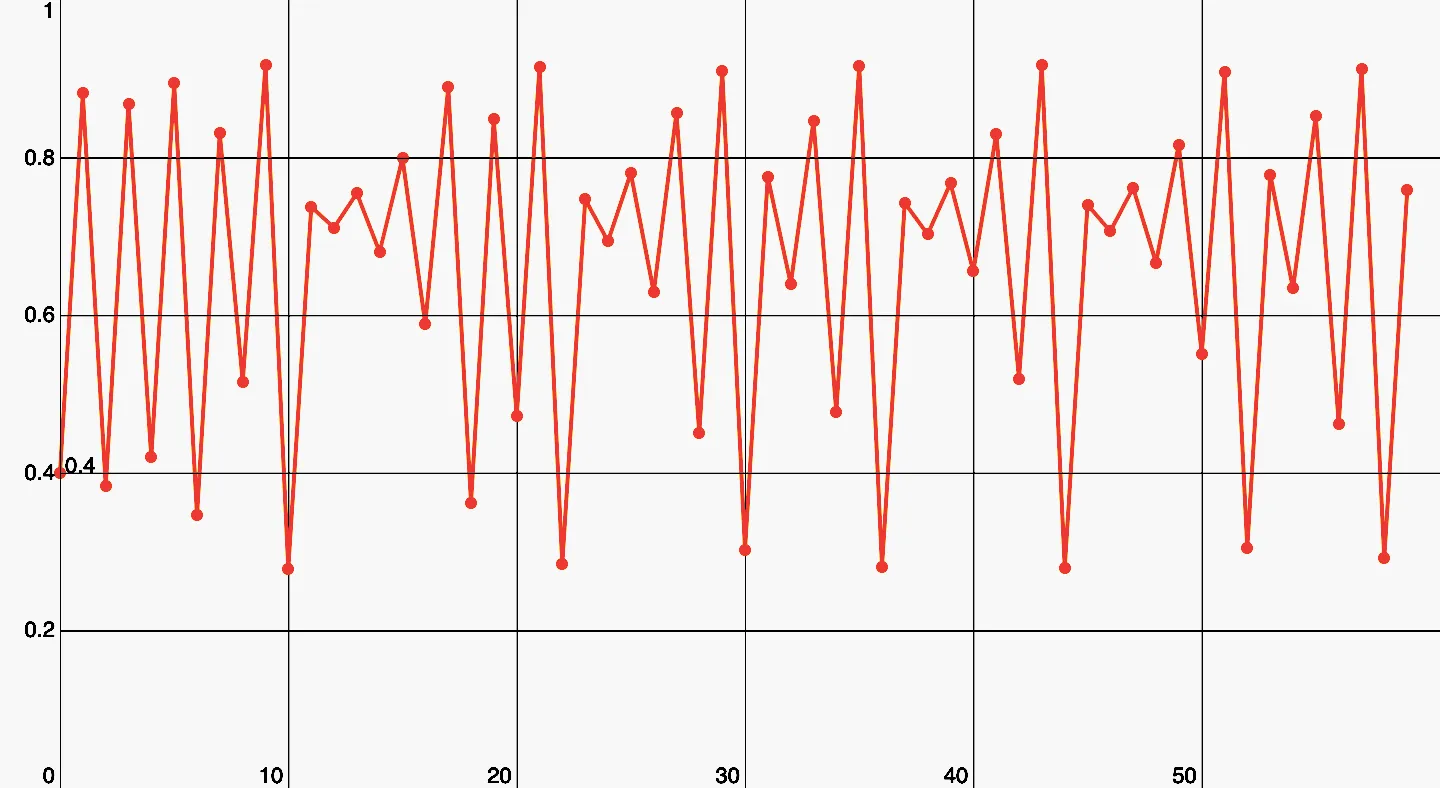
Chaos! Es ist fast schon traurig, dass nix davon zufällig ist, pure Mathematik!
Deterministisches Chaos, um genau zu sein. Hier kannst du jede Periode finden. Jedes x ist Teil irgendeiner Periode, egal ob or oder etc. Es ist deterministisches Chaos, weil man theoretisch für jeden Wert den Startwert berechnen kann und somit auch den nächsten Wert vorhersagen kann. Praktisch ist das kaum möglich, weil man jeden Wert auf unendlich viele Kommastellen genau braucht.
Genug Theorie, nun zum Programm. Als aller erstes, die Basics! Das Programm wird über die Konsole im Browser gesteuert. Durch das aufrufen von JavaScript Funktionen werden Anweisungen an das Programm geschickt
Disclaimer: Die Konsole ist (derzeit, PRs sind Willkommen) der einzige Weg dieses Programm zu kontrollieren.
Die Funktionen help() und zoomHelp() geben einen kleinen überblick über die Funktionen und ihre Anwendung, hier erkläre ich alles etwas genauer und umfassender. Wenn du das Script öffnest wird die Größe vom Browser Fenster gespeichert. Diese gespeicherte Größe wird später für das zeichnen der Graphen benötigt. Da das Programm nicht die aktuelle Größe im Auge behält, muss man die Funktion resize() aufrufen oder das Script neu laden, wenn die Größe des Browser Fensters sich geändert hat. Mit der clearScreen() Funktion wird das wird das Diagramm zurückgesetzt.
Hier habe ich einige Funktionen vorprogrammiert, damit man sich einige atemberaubend schöne Stellen der Funktion anschauen kann, ohne sich sorgen um Parameter zu machen. Diese sind plot() und plotPointx().
Mit plot() kann man sich das gesamte Diagramm anschauen. Es startet bei und geht bis . Es fängst deshalb erst bei an, weil davor nix passiert, nur eine langweilige Linie.
Bei plotPointx() hat man mehrere Optionen: plotPoint2(), plotPoint1(), plotPoint02(), plotPoint005(), plotPoint0001(), plotPoint00005(). Die Zahlenwerte repräsentieren Reichweiten von . Zum Beispiel, bei plotPoint02() ist ein bestimmter Wert von an der linken Seite des Bildschirms und auf der rechten. Um das Diagramm zeichnen zu können, muss ich über die Funktion iterieren. Die Variable iterationsbestimmt diesen Wert. Der Standartwert liegt bei , dieser kann mit der Funktion setIterations(to)verändert werden. Das Argument to wird der neue iterations-Wert sein. Ist dieser zu groß gewählt, kann das Zeichnen zu lange dauern, da dieser aber auch die Dichte der Punkte bestimmt, ist einer zu kleiner Wert auch sehr unvorteilhaft, da man dann kaum noch etwas erkennen kann.
Mit der plotRange() Funktion kann man sich jede beliebige Stelle des Diagramms ansehen. Dafür muss man aber mindestens 4 Argumente mitgeben.
Das erste heißt from. Dieses bestimmt den Wert von am linken Bildschirmrand. Der Wert sollte zwischen und liegen. Das zweite Argument ist to, dies ist der Wert von am rechten Bildschirmrand. Auch er sollte zwischen und liegen und muss dazu noch größer als from sein.
Die nächsten 2 sind minX und maxX. Hierbei kann ich zwar nicht auf bestimmte Werte beschränken, jedoch aber das Sichtfeld. Zum Beispiel wenn ich minX auf und maxX auf setzte, kann ich nicht verhindern, dass es x-Werte kleiner als und größer als gibt, jedoch kann ich diese außerhalb des Sichtfelds zeichnen. Das abändern dieser Werte von und verhindert, dass das Diagramm gedehnt oder gestaucht wird.
Das 5. Argument (iterations) ist optional und wird standartmäßig auf den Wert der iterations Variable gesetzt. Das 6. Argument (zoom) wird nur von Programm benötigt.
Falls man die derzeitige Konfiguration des Diagramms wissen will, kann man logPlot() aufrufen.
Um den Zoom-Modus zu aktivieren muss man zoomIn() aufrufen, um heraus zu zoomen zoomOut() und um ihn wieder ganz auszustellen muss du disableZoom() aufrufen. Da das Zoomen sehr aufwendige Berechnungen enthält werden die Iterationen auf einen Standartwert von herabgestellt, um eine bessere Lesitung zu liefern. Mit der Funktion setZoomInterations(to) lässt sich aber auch dieser verändern. Die Zoom-Rate kann durch die Funktion setZommRate(to) verändert werden. Der Zoomfaktor oder die Zoom-Rate ist der Faktor für das zoomen, das heißt ein Zoom-Faktor von zoomt das Diagramm x2 oder doppelt so groß.
Wenn einer der beiden Zoom-Modes aktiviert ist, kann man mit einem Klick im Diagramm zoomen. Die Stelle, die dabei angeklickt wird, wird danach in der Mitte sein. Dadurch, dass das Steuerparameter sehr “empfindlich” ist und immer innerhalb sein muss, können sehr komische Dinge oder gar nichts passieren, wenn diesen Bereich verlässt. Um dies zu verhindern, empfehle ich im Ausgangszustand (erreichbar mit plot()) nicht heraus zu zoomen oder in sehr groben Darstellung (eine Änderung von von links nach rechts von mehr als ) nicht mit einem Zoom-Faktor von 1 „herumzuschauen“.
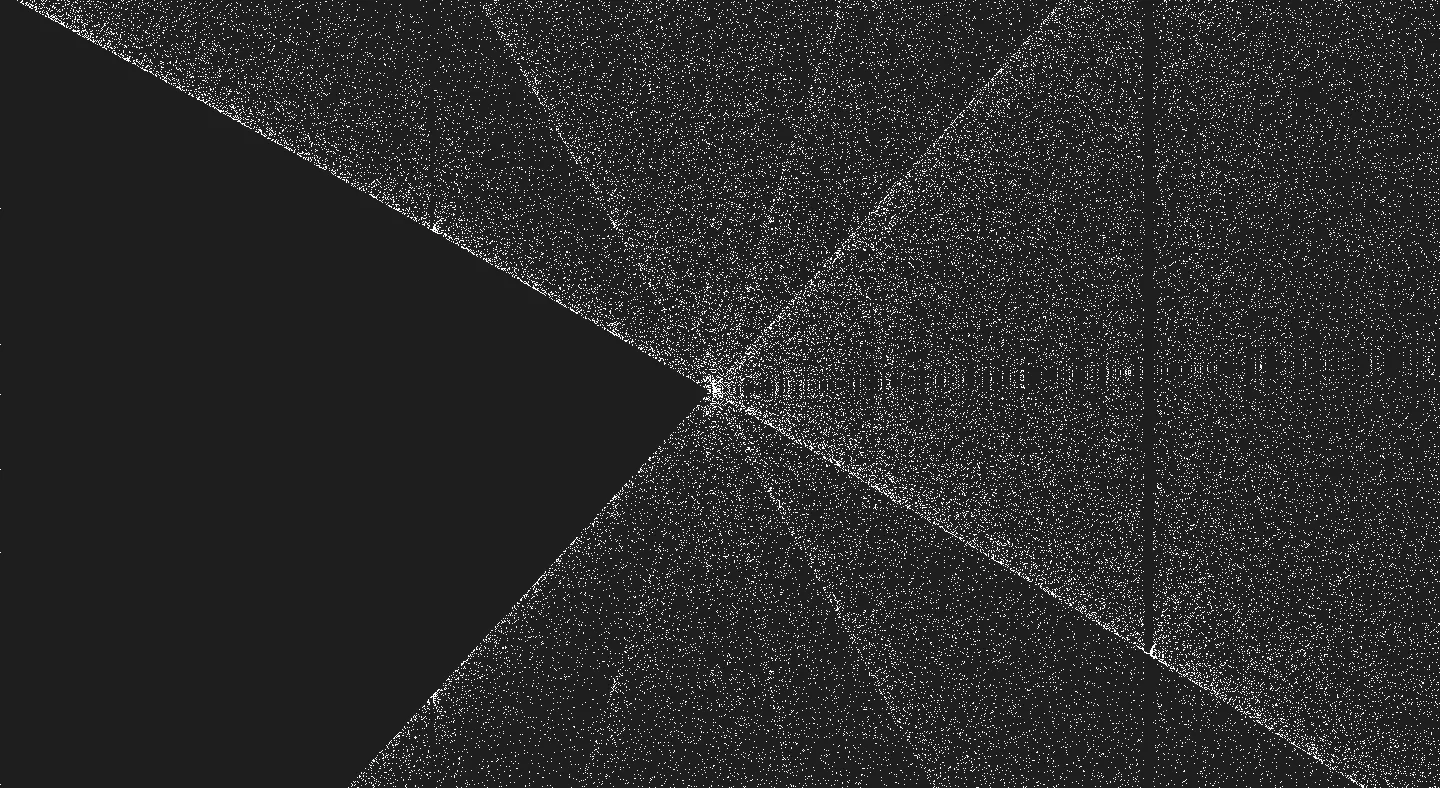

Hier ist ein Beispiel dafür, was mit zoomen möglich ist.
Das ist es schon. Ich hoffe alles ist zu verstehen. Der Quellcode zum Projekt ist auch auf Github zu finden.